Variation d'une suite
Définition :
Soit
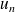une suite numérique définie sur N :
La suite
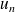est croissante à partir de l'indice p si pour tout n ≥ p,
≥
.
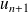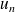La suite
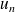est décroissante à partir de l'indice p si pour tout n ≥ p,
≤
.
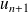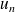La suite
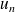est constante à partir de l'indice p si pour tout n ≥ p,
=
.
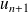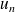Exemple :
Soit la suite
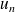définie pour tout n ∈ N par son terme général
.
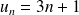Pour déterminer le sens de variation de cette suite, chercher d'abord l'expression de
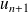
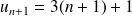
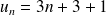
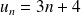
Puis calculer la différence
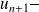
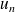
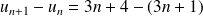
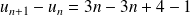
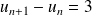
Enfin déterminer le signe de cette différence
-
:
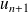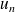Pour tout n∈N, 3 > 0 d’où
>
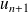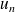, ce qui signifie que la suite
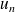est croissante.
