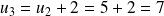Suites Arithmétiques
Suites arithmétiques
Définition:
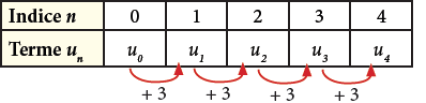
Voici une liste de nombres : -2 ; 1 ; 4 ; 7 ; 10 ; 13.
On note ,
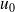= −2 ,
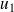= 1, etc. On constate que chaque terme est obtenu, en ajoutant 3 au terme précèdent.
Schéma d'illustration :
Définition :
On dit qu'une suite
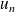est arithmétique lorsque chaque terme de la suite est obtenu en ajoutant un même réel, noté r, au terme précédent. C'est-à-dire lorsque pour tout n∈N,
.
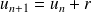Le nombre réel r s'appelle la raison de la suite.
Schéma d'illustration :
Exemple :
Soit
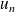une suite arithmétique de raison r = 2 et de premier terme
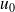=1. Cette suite est définie pour tout entier n ∈N par :
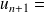
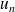+2
Ainsi,
;
;
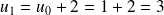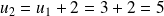