Exemple
Exemple :
Soit
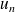une suite arithmétique de raison r = 2 et de premier terme
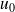=1. Cette suite est définie pour tout entier n ∈N par :
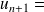
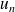+2
Ainsi,
;
;
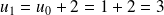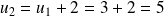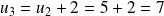
Remarque :
On dit qu'une suite arithmétique correspond à une progression linéaire : sur un graphique les points de coordonnées (
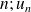) sont alignés.
Forme explicite
Propriéte :
Si une suite
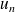est arithmétique de raison r et de premier terme
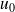, alors pour tout n ∈N, on a :
=
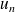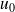+nr .
Exemple :
Soit
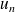la suite arithmétique de raison r = 3 et de premier terme
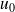= 4 , alors :
Pour tout n∈N,
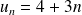. De plus
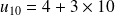
Sens de variation
Propriété :
Soit ( ) n u une suite arithmétique de raison r, alors :
Si r > 0 , la suite arithmétique est croissante.
Si r < 0 , la suite arithmétique est décroissante
