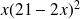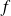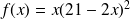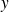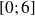25
BAC D'après Réunion, juin 2002
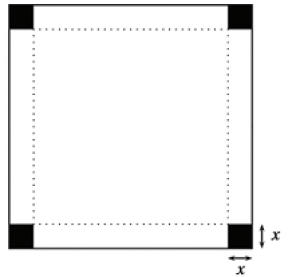
1. À partir d'une feuille de papier carrée de 21 cm de côté on veut réaliser une boîte sans couvercle, selon le schéma ci-dessous : on coupe les quatre carrés noires, de côté
a. Expliquer pourquoi
b. Justifier que le volume de la boîte en cm3 est égal à
|  |
2. On considère la fonction
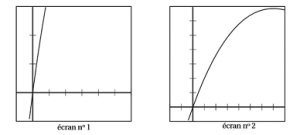
Deux élèves ont cherché à représenter cette fonction à l'aide de leur calculatrice graphique :
a. Les écrans obtenus sont représentés ci-contre. Lequel des élèves a obtenu l'écran n°1 ? b. La fonction
c. En annexe 1, on donne une représentation graphique de la fonction f obtenue à l'aide d'une calculatrice. Préciser la fenêtre utilisée. Pour cela, on pourra procéder à des essais successifs à l'aide de la calculatrice et on complétera le cadre en annexe 1. |  |
Annexe 1 Fenêtre correspondant au graphique ci-dessus :
Le pas de graduation sur l'axe des abscisses est .....
Le pas de graduation sur l'axe des ordonnées est ..... |  |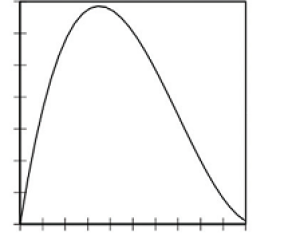
3. À l'aide d'un tableur, on a obtenu le tableau de valeurs fourni . a. Quelle formule, à recopier vers la droite jusqu'à la cellule N2, peut-on saisir dans la cellule B2 pour remplir ce tableau? b. Compléter ce tableau. |  |
4. Répondre par « vrai » ou bien par « faux » aux affirmations suivantes et argumenter chaque réponse :
a. On peut fabriquer deux boîtes différentes ayant pour volume 500 cm3.
b. On peut réaliser une boîte de volume 690 cm3.
c. Le volume le plus grand est obtenu pour une valeur de
comprise entre 3 et 4.
5. Par lecture graphique, donner le volume de la plus grande boîte réalisable, ainsi que la valeur de
correspondante
