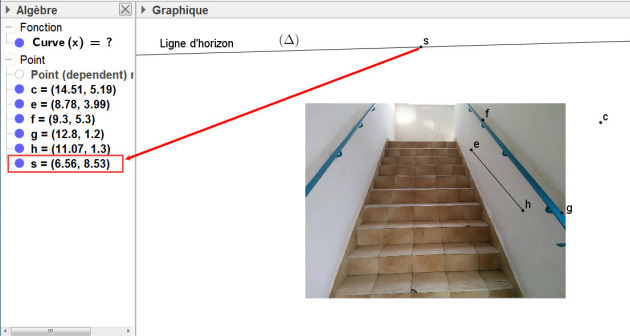
Exercice 2 (7 points)
La figure ci-contre est une photographie d'un escalier avec deux rampes d'appui. Cette photographie est une représentation en perspective centrale à un point de fuite. |  |
Question
Partie A
Construire dans l'annexe en laissant les traces de construction apparente :
le point de fuite principal noté s.
la ligne d'horizon.
Partie A
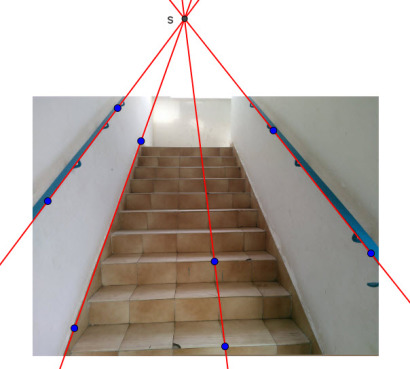
1. Dans la perspective centrale à un point de fuite, toutes les lignes de fuite de la représentation de l'objet concourent en un point de fuite unique.
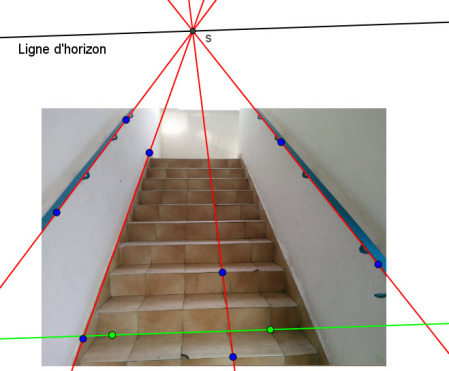
2. La droite passant par le point de fuite s et parallèle à toute droite horizontale du plan frontal, par exemple la droite (représenté en couleur verte), est la ligne d'horizon.
Question
Dans la suite de l'exercice on utilisera le fichier GeoGebra (exercice2.ggb)
Donner les coordonnées du point de fuite s.
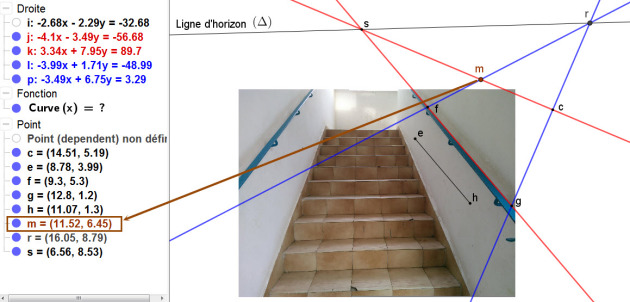
Le point e, f, g, h et c sont placés dans le fichier GeoGebra fourni.Tracer dans le fichier, la droite (fg) et en déduire une explication du fait que la rampe est bien construite.
Les droites (eh) et (gf) sont-elles parallèles ? Justifier.
Placer dans le fichier GeoGebra fourni, le point m tel que le quadrilatère fgcm soit l'image d'un parallélogramme FGCM. Donner sur la copie, les coordonnées dans GeoGebra du point m.
Partie B
1. Les coordonnées du point de fuite s sont
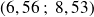
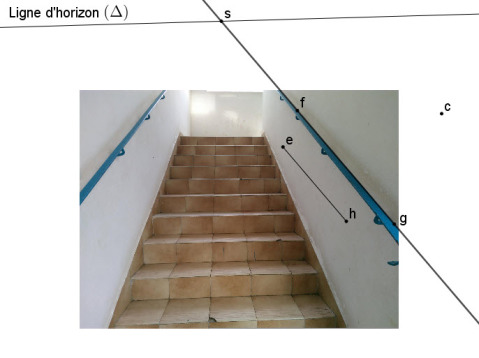
2. La droite (fg) passe par le point de fuite s (voir la figure ci-dessous). Cela montre que la rampe est bien parallèle à l'escalier.
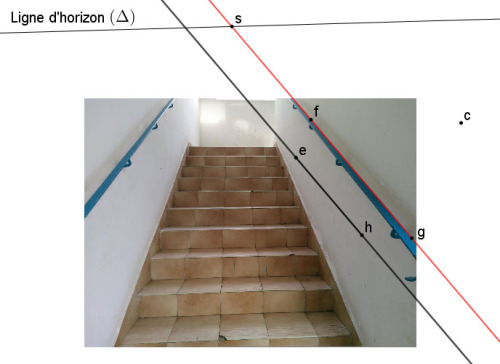
3. Les droites (eh) et (gf) ne sont pas parallèles car elles ne concourent pas vers le point fuite s.
4. Les droites (fg) et (cm) sont parallèles car elles concourent en point de fuite s. Les droites (fm) et (gc) sont parallèles car elles concourent en point de fuite r. Alors le quadrilatère fgcm est l'image d'un parallélogramme FGCM.
Les coordonnées du point m sont
.
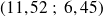