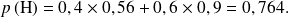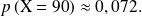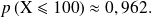Exercice 3 (5 points)
Dans tout l'exercice, on arrondira les résultats à 10-3 près.
Les parties A et B sont indépendantes.
Une étude réalisée auprès des élèves d'un lycée a permis de constater que :
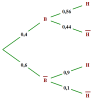
40% des élèves prennent le bus pour se rendre au lycée
parmi les élèves empruntant le bus, 56% arrivent à l'heure au lycée
10 % des élèves n'empruntant pas le bus, arrivent en retard.
Question
Partie A :
On choisit au hasard, un élève de ce lycée. On considère les événements suivants :
B : « l'élève emprunte le bus pour se rendre au lycée ».
H : « l'élève arrive à l'heure au lycée ».
Traduire par une phrase, l'événement
.
Donner un arbre de probabilité traduisant la situation.
Montrer que la probabilité que l'élève choisi soit à l'heure est
.
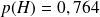Partie B :
On choisit au hasard et indépendamment les uns des autres, un groupe de 121 élèves du lycée. Soit X la variable aléatoire comptant le nombre d'élèves arrivés à l'heure dans ce groupe. On admettra que la probabilité qu'un élève arrive à l'heure est
.
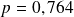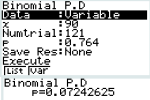
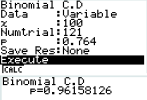
Déterminer la probabilité qu'exactement 90 élèves de ce groupe soient arrivés à l'heure au lycée.
Déterminer la probabilité qu' au plus 100 élèves de ce groupe soient arrivés à l'heure au lycée.
Partie A
$
est l'événement « l'élève choisi n'a pas pris le bus et est en retard »
Partie B
