Exercice 2 (6 points)
Dans cet exercice tous les résultats sont arrondis au centième près.
Des géologues veulent étudier les variations de température (en T°C), durant l'été, en fonction de l'altitude (en km) d'une montagne de 4 800 m d'altitudes. Les relevées des températures sont données dans le fichier Excel (exercice2.xlsx)
Question
Déterminer le taux d'évolution de la température entre les altitudes 1500m et 2500m.
On admet que le nuage des points de coordonnées
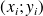peut être ajusté par une droite (d) d'équation
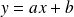.a) Quelle formule doit-on saisir dans la cellule E4 pour trouver la valeur de
.b) Quelle formule doit-on saisir dans la cellule E6 pour trouver la valeur de
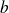.c) En déduire l'équation de la droite (d).
Selon cet ajustement, un géologue affirme que la température au sommet de la montagne est d'environ 11,6°. A-t-il raison ? justifier.
Le taux d'évolution de la température entre les altitudes 1500m et 2500m est
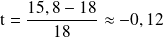.a) La formule saisie dans la cellule E4 est
=PENTE(B2:B40;A2:A40)
b) La formule saisie dans la cellule E6 est
=ORDONNEE.ORIGINE(B2:B40;A2:A40)
c) L'équation de la droite (d) est
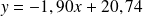
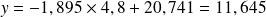
Le géologue a raison.
