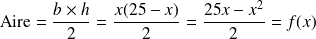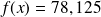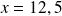Exercice 3 (7 points)
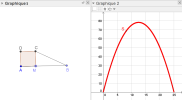
Un chef d'établissement veut agrandir sa bibliothèque. Il fait appel à un ingénieur qui lui fait un plan illustré dans le graphique 1. Le carré ADCM représente le stock et le triangle BMC celui de la bibliothèque.
Dans le graphique 1, on considère le point M appartenant au segment [AB]. On note la distance AM =
.
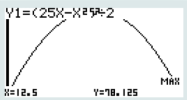
Sur le graphique 2, on donne la trace du point S d'abscisse
et d'ordonnée l'aire du triangle BMC. L'unité de mesure est le mètre.
L'objectif de l'exercice est de déterminer l'aire maximale du triangle BMC en fonction de la distance AM.
Voici une capture d'écran de la situation dans le logiciel GeoGebra.
Question
Partie A : Lecture graphique
Quel est la longueur du segment [AB] ?
Interpréter dans le contexte de l'énoncé, l'allure de la courbe décrite par la trace du point S.
Déterminer l'aire du triangle BMC lorsque le point M est confondu avec le point B.
Partie B : Recherche de l'aire maximale du triangle
Conjecturer à l'aide du fichier GeoGebra « aire.ggb », la valeur approchée à 10-3 près, de l'aire maximale du triangle BMC et de la longueur du segment [AM] correspondante.
Recopier les valeurs obtenues sur la copie.
Montrer que l'aire du triangle BMC est donnée par l'expression de la fonction
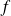définie sur [0 ; 25] par
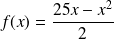.En déduire la valeur de
pour laquelle le maximum de la fonction f est atteint et la valeur du maximum de cette fonction
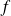.Conclure.
Partie A : Lecture graphique
La longueur du segment [AB] est 25 m.
L'aire du la bibliothèque varie en fonction de la longueur du côté du stock et présente un maximum.
l'aire du triangle BMC est nulle lorsque le point M est confondu avec le point B.
Partie B : Recherche de l'aire maximale du triangle
L'aire maximale du triangle BMC est ≈ 78,1m² lorsque la longueur du segment [AM] est ≈ 12,5 m .
l'aire du triangle BMC est :
À l'aide la calculatrice on a :
Le maximum de
pour
.
L'aire de la bibliothèque est maximale lorsque le côté du stock est 12,5 m.
