32
L'association sportive d'un lycée compte 250 élèves. Ces élèves doivent choisir un sport et un seul parmi les trois proposés: le basket-ball, le volley-ball et le football. La répartition de ces élèves se fait de la façon suivants :
Partie A :
Compléter le tableau ci-dessous.
Basket-ball
Volley-ball
Football
Total
Fille
40
50
130
Garçon
Total
66
75
250
On rencontre un élève de l'association au hasard. Tous les élèves ont la même probabilité d'être rencontrés.
On considère les événements suivants :
F « L'élève rencontré est une fille »;
B « L'élève rencontré a choisi le basket-ball ».
Calculer les probabilités suivantes :
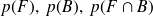 et
et
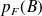 .
.a. Calculer
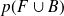 .
.b. Les événements F et B sont-ils indépendants? Justifier la réponse.
Partie B :
Soit les probabilités suivantes:
V « La probabilité que l'élève rencontré a choisi le volley-ball » ;
G « La probabilité que l'élève rencontré est un garçon » ;
D « La probabilité que l'élève rencontré est un garçon et choisi le volley-ball ».
On donne l'algorithme suivant :
Que représente les variables C et E?
a. Quelle est la valeur de C.
b. Quelle est la valeur de E.







