42
D'après Polynésie, 10 juin 2010
Un institut de recherche désire relever des informations sur l'état de l'enneigement dans un massif montagneux. Pour cela, il décide d'installer des stations de collecte de données à flanc de montagne, entre 1 200 et 3 000 m d'altitude. Chaque station sera installée 200 m plus haut que la précédente. L'institut s'adresse à un organisme qui propose d'installer la station la plus basse (située à 1 200 m d'altitude) pour un coût de 150. Le coût d'une station augmente de
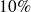à chaque fois que l'on s'élève de 200 m d'altitude.
Combien coûte une station située à 1 400 m d'altitude ?
Pour étudier la faisabilité de ce projet, On utilise un tableur, dont on extrait la feuille de calcul suivante :
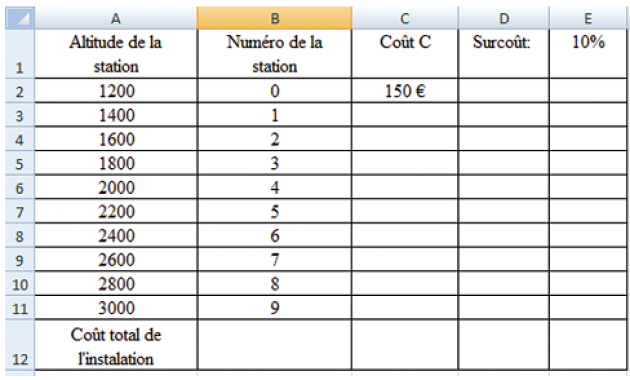
La cellule E1 est formatée en pourcentage : la valeur qu'elle contient est 0,1 et s'affiche
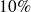. On appelle
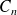le coût de la station numéro
. On a
.
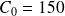a. Quelle est la nature de la suite
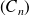? Justifier.
b. Exprimer
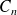en fonction de n. En déduire le coût de la station située à 2 400 m d'altitude. (On arrondira le résultat à l'entier le plus proche).
c. On veut remplir la colonne C qui indique le coût de chacune des stations.
Parmi les 4 propositions ci-dessous, choisir celle(s) que l'on peut saisir dans la cellule C3 et recopier vers le bas:
=C2*1,1 ;
=C2*(1+$E1) ;
=C2*(1+$E$1) ;
=C2*1,1ˆB3 .
d. Quelle formule peut-on saisir dans la cellule C12 pour obtenir le coût total de l'installation des stations d'étude ?
