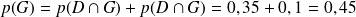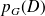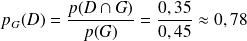Exercice Résolu 3
Une salle de jeu comporte deux consoles identiques proposant le même jeu. Un jour, l'une des deux consoles est déréglée. Les joueurs ne peuvent savoir laquelle des deux est déréglée. Ce jour-là, un joueur choisit au hasard l'une des deux consoles et il joue une partie sur cette console.
On note :
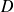l'événement « le joueur choisit la console déréglée » et
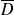l'événement contraire de
.
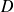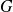l'événement « le joueur gagne la partie » et
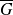l'événement contraire de
.
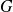Question
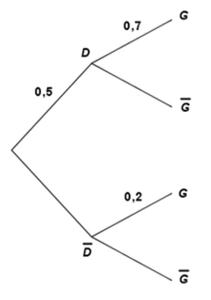
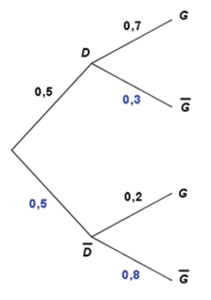
Cette situation aléatoire est modélisée par l'arbre incomplet suivant, dans lequel figurent certaines probabilités. Ainsi, 0,7 est la probabilité que le joueur gagne sachant qu'il a choisi la console déréglée.
|  |
Solution :
|  |
