Activité 2
Indépendance d'événement
On dispose des informations suivantes sur les élèves d'un lycée
Porte des lunettes | Ne porte pas des lunettes | Total | |
|---|---|---|---|
Fille | 150 | 450 | 600 |
Garçon | 100 | 300 | 400 |
Total | 250 | 750 | 1000 |
On choisit un élève au hasard parmi les 1000 élèves, en supposant qu'il y a équiprobabilité. On considère les événements suivants:
L : « L'élève choisi porte des lunettes »
, F : « L'élève choisi est une fille »
et G : « L'élève choisi est un garçon »
.
Calculer les probabilités
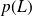et
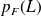. D'après ce résultat, le fait d'être une fille influe t-il sur la probabilité de porter des lunettes ?Si
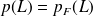alors F et L sont dits indépendants, que conclure pour F et L?Calculer les probabilités
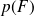et
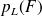. D'après ce résultat, le fait de porter des lunettes influe t-il sur la probabilité d'être une fille ?Si
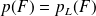alors F et L sont dits indépendants, que conclure pour F et L?Montrer que
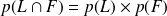.Si
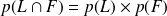alors L et F sont dits indépendants.Déterminer si G et F sont indépendants.
