10 Corrigé
Soit une fonction
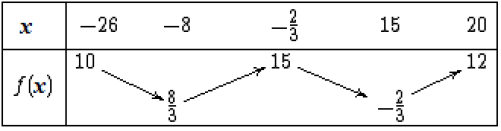
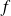définie sur [-20 ; 26] dont on donne le tableau de variations ci-dessous.
Question
Combien l'équation
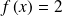a-t-elle de solutions sur l'intervalle [-20 ; 26] ?Donner un nombre ayant 4 antécédents par la fonction
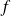?Donner un nombre ayant exactement 3 antécédents par la fonction
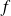.Déterminer le minimum de la fonction
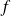sur l'intervalle[-20 ; 26], puis son maximum.a. Comparer
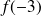et
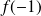.b. Comparer
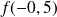et
.
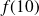Sur l'intervalle
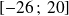l'équation
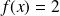admet 2 solutions.Les nombres ayant 4 antécédents sont : 3 ; 4 ; 5 ; 6 ; 7...
Les nombres ayant exactement 3 antécédents sont : 11 et 12.
Le minimum est
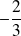et elle est atteinte en point d'abscisse 15.Le maximum est 15 et elle est atteinte en point d'abscisse
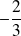.a.
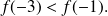
b. On ne peut pas conclure.
