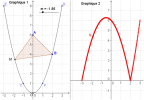
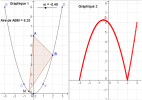
Exercice 1 : (5 points)
Le graphique 1 donne la courbe
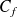représentative de la fonction
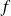définie sur l'intervalle [-3 ; 3] par
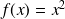.Le point M est un point mobile de la courbe
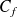d'abscisse m. Le point A a pour coordonnées (0 ; 6). Les points B, C, D, E, F et O sont les points de la courbe
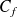d'abscisses respectives
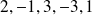et
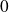. Dans le graphique 2, la trace du point S donne la représentation graphique de l'aire (en unités d'aires) du triangle ABM en fonction de m.
Question
Partie A : Lecture graphique
Interpréter l'allure de la courbe décrite par la trace du point S.
Déterminer l'aire du triangle ABM lorsque le point M est confondu avec le point E.
Déterminer les positions du point M dans le graphique 1 pour lesquels l'aire du triangle ABM vaut 6.
Partie B : Conjecture à l'aide d'un logiciel de géométrie dynamique.
À l'aide du fichier GeoGebra, donner une valeur approchée à 10-2 près de l'aire maximale du triangle ABM.
Partie A : Lecture graphique
La trace du point S montre que l'aire du triangle ABM n'est pas constante et qu'elle présente une valeur maximale.
Lorsque le point M est confondu avec le point E, l'aire du triangle ABM vaut 0.
Le point S a alors pour coordonnées (-3 ; 0).
L'aire du triangle ABM vaut 6 lorsque le point M est soit en C, soit en O ou soit en D.
Partie B : Conjecture à l'aide d'un logiciel de géométrie dynamique.
L'aire maximale vaut environ 6,25.
