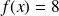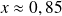Exercice 1 (7 points)
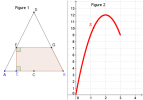
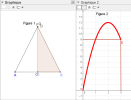
La figure 1 représente un triangle ABD isocèle en D. Le point C est le milieu du côté [AB] et CD est la hauteur du triangle ABD. Le point E est un point mobile du segment [AC].
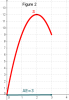
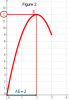
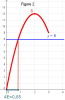
La figure 2 représente la trace du point S ayant pour abscisse la distance AE et pour ordonnée l'aire du polygone EFGB.
L'objectif est de déterminer la longueur AE pour laquelle l'aire du polygone EFBG vaut 8.
Question
Partie A : lecture graphique
Déterminer la longueur du segment [AC].
Interpréter dans le contexte de l'énoncé, l'allure de la courbe décrite par la trace du point S.
Déterminer la hauteur CD du triangle ABD.
Déterminer l'aire maximale du polygone EFGB et en déduire la distance AE correspondante.
Déterminer approximativement la longueur de [AE] pour laquelle l'aire EFGB vaut 8.
Partie B : utilisation d'outils TICE
Conjecturer à l'aide du fichier GeoGebra «exercice1.ggb», la valeur approchée à 0,01 près de la longueur de [AE] pour laquelle l'aire EFGB vaut 8.
On admet que l'aire maximale du polygone EFGB est donnée par la fonction
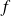définie sur [0 ; 3] par
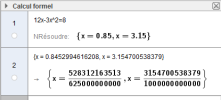
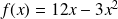. En déduire la valeur approchée de x pour laquelle
.
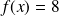Partie A : Lecture graphique
La longueur du segment [AC] est 3
La trace du point S montre que l'aire du polygone EFGB varie et qu'elle présente un maximum.
La hauteur CD vaut 6 car quand E est confondu avec le point C, le polygone devient un triangle rectangle de base 3 et d'aire 9.
L'aire maximale vaut 12 pour une distance AE = 2.
AE ≈ 0,8
Partie B : utilisation d'outils TICE
Pour AE ≈ 0,85 on a l'aire qui vaut 8.
pour
