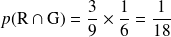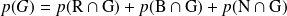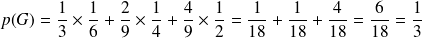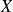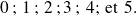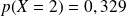Exercice 3 (7 points)
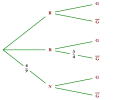
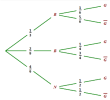
Une urne contient trois boules rouges, deux boules blanches et quatre boules noires indiscernables au toucher. On tire une boule au hasard de l'urne et on observe sa couleur :
Si la boule tirée est de couleur rouge, on lance un dé cubique équilibré dont les faces sont numérotées de 1 à 6.
Si la boule tirée est de couleur blanche, on lance un dé tétraédrique équilibré dont les faces sont numérotées de 1 à 4.
Si la boule tirée est de couleur noire, on lance une pièce de monnaie équilibrée dont les faces sont numérotées 1 et 2.
La partie est gagnée si on obtient une face portant le numéro 1.
On définit les événements R, B, N et G par :
R :
« la boule tirée est rouge »
B :
« la boule tirée est blanche »
N :
« la boule tirée est noire »
G :
« gagner la partie »
Question
Compléter l'arbre pondéré ci-dessus.
Déterminer la probabilité
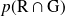.Montrer que la probabilité de gagner la partie est
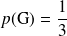.On répète cinq fois de suite cette expérience dans les mêmes conditions et on définit la variable aléatoire X donnant le nombre fois qu'on gagne la partie.
a) Quelles sont les valeurs possibles prises par la variable aléatoire X ?
b) On admettra que la variable aléatoire X suit une loi binomiale. Préciser ses paramètres.
c) Déterminer la probabilité de gagner exactement deux fois.
(On donnera le résultat arrondi à 10–3près.)
.a) Les valeurs prises par
sont :
b)X suit une loi binominale de paramètres
.c.
.
