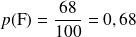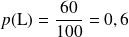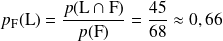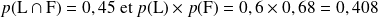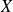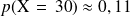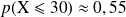Exercice 1 (5 points)
Le club de lecture d'un lycée compte 100 adhérents. Leur répartition est décrite dans le tableau ci-dessous :
Garçons | filles | |
|---|---|---|
Série L | 15 | 45 |
Autres séries | 23 | 17 |
On choisit un adhérent au hasard.
On considère les événements suivants :
G l'événement :
« l'adhérent choisi est un garçon »
;F l'événement :
« l'adhérent choisi est une fille »
;L l'événement :
« l'adhérent choisi est en série L »
.
Question
Partie A
Dans cette partie, on donnera les valeurs exactes de chaque probabilité.
a) Calculer la probabilité de l’événement F.
b) Calculer la probabilité de l’événement L.
a) Déterminer la probabilité que l'adhérent choisi soit en série L sachant que c'est une fille.
b) Les événements F et L sont-ils indépendants ? Justifier la réponse.
Partie B
Dans cette partie, on donnera les valeurs approchées de chaque probabilité à 10-2près.
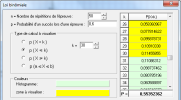
On interroge au hasard et de façon indépendante 50 adhérents. On définit la variable aléatoire X donnant le nombre d'adhérents qui sont en série L.
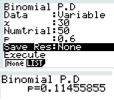
Montrer que X suit une loi binomiale et préciser ses paramètres.
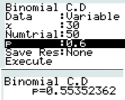
Calculer la probabilité
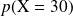 et
et
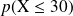 .
.