Manuel Numérique de Mathématiques Informatique Terminale L

Cours
Outils

Exercice 3 (6 points)

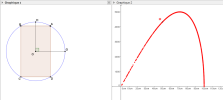
Ali veut couper une planche rectangulaire ABCD d'aire maximale dans un contre-plaqué circulaire de diamètre un mètre.

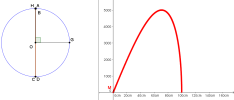
Dans le graphique 1, (∆) est un cercle de rayon 50 cm. Les droites OH et OG sont perpendiculaires. A est un point libre de l'arc 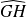. ABCD est un rectangle inscrit dans le cercle (Δ). On note la distance AB.

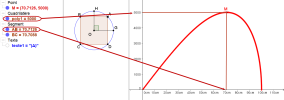
Dans le graphique 2, la trace du point M donne la représentation de l'aire du rectangle ABCD en fonction de la distance AB.

Question

Exercice3.ggb

On utilisera le fichier numérique « Exercice3.ggb » Télécharger le fichier ci-dessus.

Quelle est la position du point A lorsque le point M a pour coordonnées (0 ; 0) ?
Donner une valeur approchée de l'aire du rectangle ABCD, lorsque la distance AB ≈ 50 cm.
Donner une valeur approchée de la distance AB, lorsque l'aire du rectangle ABCD est environ 2 000 cm².
Interpréter l'allure de la courbe décrite par la trace du point M dans le contexte de l'énoncé.
a) Déterminer l'aire maximale du rectangle ABCD.
b) En déduire une valeur approchée de la longueur du segment [AB].

Solution

Lorsque le point M a pour coordonnées (0 ; 0), le point A est confondue avec le point H.
Pour 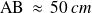, l'aire du rectangle ABCD vaut environ .
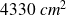Lorsque l'aire du rectangle ABCD est environ 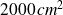, la distance .
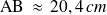L'aire du rectangle varie en fonction de la distance AB et présente une valeur maximale.
.a) L'aire maximale du rectangle .
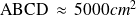b) L'aire est maximale pour .

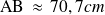Accueil

Imprimer