40
D'après BAC L, Polynésie, juin 2010.
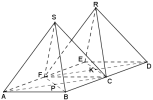
On a représenté sur la figure 1 ci-dessous en perspective parallèle deux pyramides régulières à base carrée SABCF et RFCDE, de même hauteur SP et RK, P étant le centre du carré ABCF et K le centre du carré CDEF.
Le plan horizontal contient les six points A, B, C, D, E et F.
Les points A et B sont dans un plan frontal. Dans tout l'exercice, on notera a, b, c, ... les images des points A, B, C.... dans cette perspective centrale.
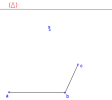
Sur la figure 2 ci-dessous, on a tracé la ligne d'horizon, notée (∆), les segments [ab] et [bc] ainsi que le point s.
Figure 1 | Figure 2 |
|---|---|
Placer le point de fuite m de la droite (bc) et le point de fuite n de la droite (ac).
Construire l'image f du point F. Donner deux propriétés de la perspective centrale qui justifient la construction du point f.
Construire les points d et e images respectives des points D et E.
Quel est le point de fuite de la droite (sr) ? On ne demande pas de justification.
Terminer la construction des deux pyramides.