16 Corrigé
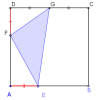
ABCD est un carré. Le point G est le milieu du segment [DC]. Le point E est un point du segment [AB]. On note
la distance AE.
Le point F est un point du segment [AD] tel que DF = AE =
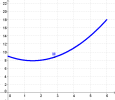
. Dans le repère ci-dessus, la trace du point M donne la représentation
de l'aire du triangle EFG en fonction de la distance AE.
|
|
Question
Partie A : Lecture graphique : ABCD
Déterminer la longueur du coté [AB].
Déterminer l'aire maximale du triangle EFG. En déduire alors la position des points E et F.
Interpréter l'allure de la courbe décrite par la trace du point M
Partie B : Recherche de l'aire minimale du triangle EFG.
Conjecture à l'aide d'un logiciel de géométrie dynamique.
a. Construire le carré ABCD de côté 6 cm et le triangle EFG en respectant les contraintes de l'énoncé.
« Appeler le professeur »
b. Représenter dans un repère la trace du point M d'abscisse
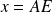et d'ordonnée l'aire du triangle EFG. « Appeler le professeur »
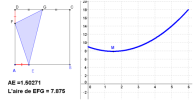
c. Déterminer les valeurs approchées au dixième près de l'aire minimale du triangle EFG et de la distance AE correspondante.
Démonstration
a. Montrer que l'aire
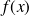du triangle EFG est telle que, pour
de l'intervalle
,
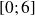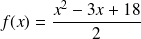
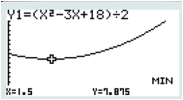
b. En déduire la valeur de
pour laquelle le minimum de la fonction
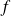est atteint et la valeur du minimum de cette fonction
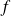.c. Conclure
Partie A : Lecture graphique:
Le coté [AB] mesure 6 cm.
L'aire maximale du triangle EFG est 18 cm². En déduire alors la position des points E et F.L'aire du triangle EFG est maximale lorsque le point E est en B et que le point F est en A.
La trace du point M montre que l'aire du triangle EFG n'est pas constante et qu'elle présente une valeur maximale.
Partie B : Recherche de l'aire minimale du triangle EFG.
EFG a une aire maximal d'environ 7,9 lorsque
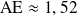.a. L'aire du triangle rectangle AEF vaut
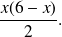
L'aire du triangle rectangle FDG vaut
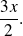
L'aire d trapèze EBCG vaut
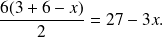
L'aire du carré ABCD vaut 36.
Donc l'aire du triangle EFG vaut :
.b.
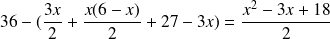c. L'aire du triangle EFG prend une valeur minimale de 7,875 cm² lorsque la distance AE = 1,5 cm.
