22
ABCD est un rectangle tel que
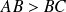. Le point E est un point du segment [DC]. On note
la distance DE. Le point F est un point du segment [BC] tel que CF = DE =
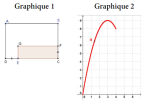
. Dans le repère ci-dessous, la trace du point M donne la représentation de l'aire du rectangle EGFC en fonction de la distance DE.
|
Partie A : Lecture graphique :
Déterminer la longueur du coté [BC] puis du coté [DC]
Déterminer l'aire maximale du rectangle EGFC. En déduire alors les positions respectives des points E et F sur le segment [DC] et sur le segment [BC].
Interpréter l'allure de la courbe décrite par la trace du point M.
Partie B : Démonstration
Montrer que l'aire
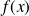du triangle EFG est telle que, pour
de l'intervalle
,
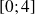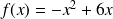.En déduire la valeur de
pour laquelle le maximum de la fonction
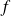est atteint et la valeur du maximum de cette fonction
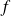.Conclure
